Hypothesis Testing: The z-test

Steps in hypothesis testing

SAT scores are normally distributed with a mean (m) of 500 and a standard deviation (s) of 100. A researcher tests the claim that using subliminal tapes can improve SAT performance. A random sample of 100 students listens to a subliminal tape intended to improve SAT scores every night for one month. All students then take the SAT. The mean SAT score for the sample (X) is 520. Do the tapes improve performance? Test at a = .05.

(1) State statistical hypotheses.

                H₀: m < 500  (subliminal tapes do not improve SAT scores)

                H₁: m > 500  (subliminal tapes do improve SAT scores)

(2) Determine rejection region & state decision rule.     

                a = .05, one-tailed z-test       

                Look up .05 in column C of unit normal table ® critical z  = +1.65

                Rejection region is area to the right of z = +1.65.

                Decision rule:  If observed z is > +1.65, then reject Ho

 (3) Compute test statistic (z).

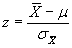
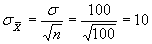
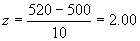
(4) Make a decision: The observed value of z = 2.00 falls in the rejection region [z observed  (2.00) > z critical (1.65)].  This is a very unlikely value (p < .05) of z if Ho is true, therefore reject Ho.

(5) State conclusions: There is sufficient evidence to conclude that subliminal tapes improve SAT scores, z = 2.00, p < .05, one-tailed.

Decisions in Hypothesis Testing

Alpha, Beta, & Power

Alpha (a) = probability of a Type I error if Ho is true

Beta (b) = probability of a Type II error if Ho is false               

Power = 1 - b = probability of rejecting Ho when it is false = ability to detect real effects

 The power of a statistical test is influenced by:

Alpha – As a increases, the rejection region increases, so you are more likely to reject Ho. That is, you have greater power to find small effects. However, you also increase the risk of type I errors.

Sample size – As n increases, the sample becomes more representative of the population and power increases.

One- vs. two-tailed tests – two-tailed tests are more conservative and therefore less powerful.